Valuation ring

In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x⁻¹ belongs to D.

Given a field F, if D is a subring of F such that either x or x⁻¹ belongs to D for every x in F, then D is said to be a valuation ring for the field F or a place of F. Since F is in this case indeed the field of fractions of D, a valuation ring for a field is a valuation ring. Another way to characterize the valuation rings of a field F is that valuation rings D of F have F as their field of fractions, and their ideals are totally ordered by inclusion; or equivalently their principal ideals are totally ordered by inclusion. The valuation rings of a field are the maximal elements of the local subrings partially ordered by dominance, where

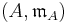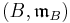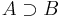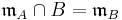$(A,\mathfrak{m}_A)$ dominates $(B,\mathfrak{m}_B)$ if $A \supset B$ and $\mathfrak{m}_A \cap B = \mathfrak{m}_B$ .

In particular, every valuation ring is a local ring.

1 Examples
2 Definitions
3 Units and maximal ideals
4 Value group
5 Integral closure
6 Principal ideal domains
7 References

Examples

Any field is a valuation ring.

Z_(p), the localization of the integers Z at the prime ideal (p), consisting of ratios where the numerator is any integer and the denominator is not divisible by p. The field of fractions is the field of rational numbers Q.

The ring of meromorphic functions on the entire complex plane which have a Maclaurin series (Taylor series expansion at zero) is a valuation ring. The field of fractions are the functions meromorphic on the whole plane. If f does not have a Maclaurin series then 1/f does.

Any ring of p-adic integers Z_p for a given prime p is a local ring, with field of fractions the p-adic numbers Q_p. The algebraic closure Z_p^cl of the p-adic integers is also a local ring, with field of fractions Q_p^cl. Both Z_p and Z_p^cl are valuation rings.

Let k be an ordered field. An element of k is called finite if it lies between two integers n<x<m; otherwise it is called infinite. The set D of finite elements of k is a valuation ring. The set of elements x such that x ∈ D and x⁻¹∉D is the set of infinitesimal elements; and an element x such that x∉D and x⁻¹∈D is called infinite.

The ring F of finite elements of a hyperreal field *R is a valuation ring of *R. F consists of all hyperreal numbers differing from a standard real by an infinitesimal amount, which is equivalent to saying a hyperreal number x such that −n < x < n for some standard integer n. The residue field, finite hyperreal numbers modulo the ideal of infinitesimal hyperreal numbers, is isomorphic to the real numbers.

Definitions

There are several equivalent definitions of valuation ring. For a subring D of its field of fractions K the following are equivalent:

For every nonzero x in K, either x in D or x⁻¹ in D
The ideals of D are totally ordered by inclusion
The principal ideals of D are totally ordered by inclusion
There is a totally ordered abelian group G (called the value group) and a surjective group homomorphism (called the valuation) ν:K^×→G with D = { x in K : ν(x) ≥ 0 } ∪ {0}

The equivalence of the first three definitions follows easily. A theorem of (Krull 1939) states that any ring satisfying the first three conditions satisfies the fourth: take G to be the quotient K^×/D^× of the unit group of K by the unit group of D, and take ν to be the natural projection. Even further, given any totally ordered abelian group G, there is a valuation ring D with value group G.

Very rarely, valuation ring may refer to a ring that satisfies the second or third condition but is not necessarily a domain. A more common term for this type of ring is "uniserial ring".

Units and maximal ideals

The units, or invertible elements, of a valuation ring are the elements x such that x⁻¹ is also a member of D. The other elements of D, called nonunits, do not have an inverse, and they form an ideal M. This ideal is maximal among the (totally ordered) ideals of D. Since M is a maximal ideal, the quotient ring D/M is a field, called the residue field of D.

Value group

The units D^* of D comprise a group under multiplication, which is a subgroup of the units F^* of F, the nonzero elements of F. These are both abelian groups, and we can define the quotient group V = F^*/D^*, which is the value group of D. Hence, we have a group homomorphism ν from F^* to the value group V. It is customary to write the group operation in V as +.

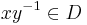We can turn V into a totally ordered group by declaring the residue classes of elements of D as "positive". More precisely, V is totally ordered by defining $[x] \geq [y]$ if and only if $x y^{ - 1 } \in D$ where [x] and [y] are equivalence classes in V.

Valuation

We add to V the special value ∞, defined to be larger than any other element of V, and such that x+∞ = ∞ for all x. If we then define ν(0) = ∞, i.e., making zero larger in value than anything else, we have the following properties:

ν(x) = ∞ if and only if x=0
ν(xy) = ν(x) + ν(y)
ν(x+y) ≥ min(ν(x), ν(y))

These are precisely the properties of a valuation, and the study of valuations is essentially the study of valuation rings.

Construction

For a given totally ordered abelian group G and a residue field k, define K = k((G)) to be the ring of formal power series whose powers come from G, that is, the elements of K are functions from G to k such that the support (the elements of G where the function value is not the zero of k) of each function is a well-ordered subset of G. Addition is pointwise, and multiplication is the Cauchy product or convolution, that is the natural operation when viewing the functions as power series:

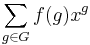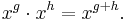
$\sum_{g \in G} f(g) x^g$ with $x^g \cdot x^h = x^{g%2Bh}.$

The valuation ν(f) for f in K is defined to be the least element of the support of f, that is the least element g of G such that f(g) is nonzero. The f with ν(f)≥0 (along with 0 in K), form a subring D of K that is a valuation ring with value group G, valuation ν, and residue field k. This construction is detailed in (Fuchs & Salce 2001, pp. 66–67), and follows a construction of (Krull 1939) which uses quotients of polynomials instead of power series.

Height of a value group

If G is a totally ordered group, a subgroup U of G is called an isolated subgroup of G if 0 ≤ y ≤ x and x ∈ U implies y ∈ U. The set of isolated subgroups is totally ordered by inclusion. The height or rank r(V) of V is defined to be the cardinality of the set of proper isolated subgroups of V. The most important special case is height one, which is equivalent to V being a subgroup of the real numbers under addition (or equivalently, of the positive real numbers under multiplication.) A value ring with a valuation of height one has a corresponding absolute value defining an ultrametric place. There is a correspondence of the isolated proper subgroups of the value group of a valuation and the prime ideals of the valuation ring. This implies that a valuation ring is discrete if and only if it is Noetherian.

The rational rank rr(V) is defined as the rank of the value group as an abelian group

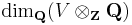$\mathrm{dim}_\mathbf{Q}(V \otimes_\mathbf{Z} \mathbf{Q})$ .

Integral closure

A valuation ring is always integrally closed. Here, an integral domain D which is integrally closed in its field of fractions is said to be integrally closed. This means that if a member x of the field of fractions F of D satisfies an equation of the form xⁿ + a₁xⁿ⁻¹ + ... + a₀ = 0, where the coefficients a_i are elements of D, then x is in D.

To see that valuation rings are integrally closed, suppose that xⁿ + a₁x^n − 1 + ... + a₀ = 0. Then dividing by xⁿ⁻¹ gives us x = − a₁ − ... − a₀x^− n + 1. If x were not in D, then x^-1 would be in D and this would express x as a finite sum of elements in D, so that x would be in D, a contradiction.

Principal ideal domains

A principal ideal domain, or PID, is an integral domain in which every ideal is a principal ideal. A PID with only one non-zero maximal ideal is called a discrete valuation ring, or DVR, and every discrete valuation ring is a valuation ring. A valuation ring is a PID if and only if it is a DVR or a field. A value group is called discrete if and only if it is isomorphic to the additive group of the integers, and a valuation ring has a discrete valuation group if and only if it is a discrete valuation ring.

References

Nicolas Bourbaki, Commutative Algebra, Addison-Wesley, 1972
Fuchs, László; Salce, Luigi (2001), Modules over non-Noetherian domains, Mathematical Surveys and Monographs, 84, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1963-0, MR 1794715
Krull, Wolfgang (1939), "Beiträge zur Arithmetik kommutativer Integritätsbereiche. VI. Der allgemeine Diskriminantensatz. Unverzweigte Ringerweiterungen", Mathematische Zeitschrift 45 (1): 1–19, doi:10.1007/BF01580269, ISSN 0025-5874, MR 1545800